2007. május 2. rész
EGYENLETEK
13.
a) Oldja meg a 7 + x < −2 ⋅ (x − 2) egyenlőtlenséget a valós számok halmazán!
2p7 + x < −2 ⋅ (x − 2) |Zfb.
7 + x < x + |+?x
7 + x < |-?
x < |:?
x <
b) Oldja meg az x² + x − 6 ≤ 0 egyenlőtlenséget a valós számok halmazán!
4p
x² + x − 6 = 0 egyenlet gyökei:
x1 =
x2 =
A főegyüttható előjele: .
A megoldásintervallum: [; ]
x² + x − 6 = 0 egyenlet gyökei:
x1 =
x2 =
A főegyüttható előjele: .
A megoldásintervallum: [; ]
c) Legyen az A halmaz a 7 + x < −2 ⋅ (x − 2) egyenlőtlenség valós megoldásainak halmaza,
B pedig az x² + x − 6 ≤ 0 egyenlőtlenség valós megoldásainak halmaza.
Adja meg az A ∪ B , A ∩ B és B \ A halmazokat! 6p
A ⋃ B = {x ∈ R | x ≤ 2}
A ⋂ B = [-3; -1[
B \ A = [-1; 2]
Adja meg az A ∪ B , A ∩ B és B \ A halmazokat! 6p
A ⋃ B = {x ∈ R | x ≤ 2}
A ⋂ B = [-3; -1[
B \ A = [-1; 2]
GRÁFOK
14.
A városi középiskolás egyéni teniszbajnokság egyik csoportjába hatan kerültek: András, Béla, Csaba, Dani, Ede és Feri. A versenykiírás szerint bármely két fiúnak pontosan egyszer kell játszania egymással.
Eddig András már játszott Bélával, Danival és Ferivel.
Béla játszott már Edével is. Csaba csak Edével játszott, Dani pedig Andráson kívül csak Ferivel.
Ede és Feri egyaránt két mérkőzésen van túl.
a) Szemléltesse gráffal a lejátszott mérkőzéseket! 4p
|
|
b) Hány mérkőzés van még hátra?
3p
Az összes mérkőzések száma =
Az hátralévő mérkőzések száma =
Az összes mérkőzések száma =
Az hátralévő mérkőzések száma =
KOMBINATORIKA
c) Hány olyan sorrend alakulhat ki, ahol a hat versenyző közül Dani az első két hely valamelyikén végez?
5pHa Dani az első helyen végez, akkor a lehetőségek száma =
Ha Dani az második helyen végez, akkor a lehetőségek száma =
Így a kérdéses lehetőségek száma =
TÉRGEOMETRIA
15.
Egy gyertyagyárban sokféle színű, formájú és méretű gyertyát készítenek. A folyékony, felhevített viaszt különféle formákba öntik.
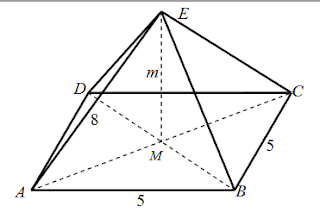
Az öntőhelyek egyikén négyzet alapú egyenes gúlát öntenek, melynek alapéle 5 cm, oldaléle 8 cm hosszú.
a) Számítsa ki ennek a gúla alakú gyertyának a térfogatát!
(Az eredményt cm³-ben, egészre kerekítve adja meg!) 4p
Ábra:
e = a · = cm
Pitagorasz-tétel (AME háromszögre): ² = m² + ²
m = cm
A gúla alakú gyertya térfogata:cm³
Ezen az öntőhelyen az egyik műszakban 130 darab ilyen gyertyát gyártanak.
b) Hány liter viaszra van szükség, ha tudjuk, hogy a felhasznált anyag 6%-a veszteség?
(Az eredményt egy tizedes jegyre kerekítve adja meg!) 4p
Az x térfogatú viasz esetén:
x = V
x = cm³
x = liter
b) Hány liter viaszra van szükség, ha tudjuk, hogy a felhasznált anyag 6%-a veszteség?
(Az eredményt egy tizedes jegyre kerekítve adja meg!) 4p
Az x térfogatú viasz esetén:
x = V
x = cm³
x = liter
VALSZÁM
A gúla alakú gyertyákat egyenként díszdobozba csomagolják. c) Hány cm² papír szükséges 40 darab díszdoboz elkészítéséhez, ha egy doboz papírszükséglete a gúla felszínének 136%-a? 4p
Az oldallap magassága (Pitagorasz tétel ): mo² = ² + ²
mo = cm
A palást területe: P = cm²
A gúla felszíne: A = cm²
A teljes felhasznált papírmennyiség: A* = cm²
NÉV:
JEGY:
| Feladat | Max p | Kapott p | Param | Be |
| 13a | 2 | |||
| 13b | 4 | |||
| 13c | 6 | |||
| 14a | 4 | |||
| 14b | 3 | |||
| 14c | 5 | |||
| 15a | 4 | |||
| 15b | 4 | |||
| 15c | 4 | |||
| Összesen: | 36 |