2010. június 1. rész

2010. június Matematika - középszint I.

1.

Egy derékszögű háromszög átfogója 17 cm, egyik befogója 15 cm hosszú.
Hány cm hosszú a háromszög harmadik oldala?

A háromszög harmadik oldala cm hosszú.

 2 pont 

2.

Az alábbi oszlopdiagramon százasokra kerekítve ábrázolták az adatokat.

év	1995.	1996.	1997.	1998.	1999.
házasságkötések száma	53500	48900	46900	44900	45500

Hány házasságkötéssel volt kevesebb 1998-ban, mint 1995-ben?

házasságkötéssel volt kevesebb.

 2 pont 

3.

Az a vektor koordinátái (2; 3), a b vektoré pedig (-1; 2).
Adja meg az a + b vektor koordinátáit!

Az a+b vektor koordinátái: ( ; )

 2 pont 

4.

Milyen x valós számra igaz, hogy 3^{x +2} = 1 ?

x =

 2 pont 

5.

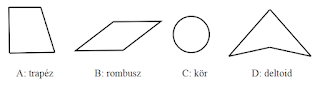
Válassza ki az alábbi 4 alakzat közül a középpontosan szimmetrikusakat, és írja be betűjelüket az erre a célra szolgáló keretbe!

A: trapéz  B: rombusz  C: kör  D: deltoid

A betűjelek: ;

 2 pont 

6.

Adja meg az x ↦ 5x -3 ( x∈R ) függvény zérushelyét!

A függvény zérushelye: x =

 2 pont 

7.

Egy négyzet alapú hasáb alapéle 3 cm.
Térfogata 72 cm³.
Hány cm hosszú a hasáb magassága?

A hasáb magassága cm hosszú.

 2 pont 

8.

Hány fényév a 47,3 milliárd km, ha 1 fényév 9460 milliárd km?
Írja le a számítás menetét!

47,3 milliárd km = / = fényév

 2 pont 

9.

Adja meg az x² + (y +1)² -4 = 0 egyenletű kör középpontjának koordinátáit és a kör sugarát!

A kör középpontjának koordinátái: (;)
A kör sugara:

 2 pont 

10.

Egy háromelemű, pozitív egészekből álló adathalmaz átlaga 3 és mediánja 2.
Adjon meg egy ilyen adathalmazt elemeinek felsorolásával!

Adatok növekvő sorrendben:
, , .

 2 pont 

11.

Egy településen a polgármester választáson 12 608 választásra jogosult közül 6347-en adtak le érvényes szavazatot.
A két jelölt egyike 4715 szavazatot, a másik 1632 szavazatot kapott.
A választásra jogosultak közül véletlenszerűen kiválasztunk egy választópolgárt.
Mekkora annak a valószínűsége, hogy a kiválasztott személy érvényesen szavazott, mégpedig a vesztes jelöltre?

k =
n =
p = %

 2 pont 

12.

Egy húrtrapéz (egyenlő szárú trapéz) egyik alapjának hossza 7cm, ezen az alapon fekvő szögei 60°-osak.
A trapéz szárai 4cm-esek.
Számítsa ki a másik alap hosszát!
Számítását részletezze!

Ábra:

x = A szárnak az alapra eső merőleges vetülete.
x =
A másik alap hossza cm.

 2 pont 

Matematika középfokú érettségi (2010.június)

NÉV:

EREDMÉNYEK:

Feladat	Max pont	Elért pont	Paraméterek	Bemenet
1.	2
2.	2
3.	2
4.	3
5.	2
6.	2
7.	2
8.	2
9.	3
10.	3
11.	4
12.	3
Össz.	30		-	-