Főoldal (Középszintű matematika érettségik)

Év	Május	Idegen nyelvű	Október	Egyéb
2022.	2022_05 ✓ 2022_05_2 ✓	2022_06 ✓	2022_10 ✓	2022_02 PDF
2021.	2021_05 ✓ 2021_05_2 ✓	2021_06 ✓	2021_10 ✓	2021_02 PDF
2020.	2020_05_1 ✓ 2020_05_2 ✗	2020_06 ✓	2020_10 ✓	2020_02 PDF 2020_02 próba ✗
2019.	2019_05_1 ✓ 2019_05_2 ✗	2019_06 ✓	2019_10 ✓	2019_02 PDF 2019_02 próba ✗
2018.	2018_05_1 ✓ 2018_05_2 ✗	2018_06 ✓	2018_10 ✓	2018_02 PDF
2017.	2017_05 ♥ 2017_05 ✓ 2017_05_2 ✓	2017_06 ✓	2017_10 ✓	2017_02 PDF
2016.	2016_05 ✓ 2016_05_2 ✓	2016_06 ✓	2016_10 ✓	Egyéb
2015.	2015_05 ✓ 2015_05_2 ✓	2015_06 ✓	2015_10 ✓	Egyéb
2014.	2014_05 ✓ 2014_05_2 ✓	2014_06 ✓	2014_10 ✓	Egyéb
2013.	2013_05 ✓ 2013_05_2 ✓	2013_06 ✓	2013_10 ✓	Egyéb
2012.	2012_05 ✓ 2012_05_2 ✓	2012_06 ✓	2012_10 ✓	Egyéb
2011.	2011_05 ✓ 2011_05_2 ✓	2011_06 ✓	2011_10 ✓	Egyéb
2010.	2010_05 ✓ 2010_05_2 ✓	2010_06 ✓	2010_10 ✓	Egyéb
2009.	2009_05 ✓ 2009_05_2 ✓	2009_06 ✓	2009_10 ✓	Egyéb
2008.	2008_05 ✓ 2008_05_2 ✓	2008_06 ✓	2008_10 ✓	Egyéb
2007.	2007_05 ✓ 2007_05_2 ✓	2007_06 ✓	2007_10 ✓	Egyéb
2006.	2006_05 ✓ 2006_05_2 ✓	2006_06 ✓	2006_10 ✓	2006_2 ⊕
2005.	2005_05 ✓ 2005_05_2 ✓ 2005_05_3 ✓	2005_06 ✓	2005_10 ✓	2005_07 ⊕
2003/2004. (minta)	-	-	-	2004 ⊕ 2003 ⊕
NKP. (próba)	-	-	-	1. feladatsor 2. feladatsor 1. feladatsor 2. feladatsor 1. feladatsor

Tömörített PDF letöltés: Feladatsorok

2022. október 1. rész

2022. október Matematika - középszint I.

1.

Adott a pozitív egész számok halmazának két részhalmaza:
A = {12-nál|-nél kisebb prímszámok},
B = {3-val|-vel nem osztható egyjegyű számok}.
Elemei felsorolásával adja meg az A, a B, az A ∩ B ésa B \A halmazokat!

A = {}
B = {}
A ∩ B = {}
B \ A = {}

 2 pont 

2.

Hány olyan háromjegyű pozitív egész szám van, melynek mindhárom számjegye nagyobb 5-nál|-nél?

Dobozmodell:
··
A megfelelő számok száma =

 2 pont 

3.

Adja meg n értékét úgy, hogy az alábbi egyenlőség igaz legyen!

27· 26	= 2n
23

n =

 2 pont 

4.

Egy 35 g tömegű csokoládészelet csomagolásán az olvasható, hogy 100 g termék 520 kcal energiát tartalmaz.
Hány kcal energiát tartalmaz ez a csokoládészelet?

A csokoládészelet kcal energiát tartalmaz.

 2 pont 

5.

Az alábbi ábrán a [ -3; 2]zárt intervallumon értelmezett x ↦ -(x +1)² + 5 függvény grafikonja látható.
Adja meg a függvény értékkészletét és maximumának helyét!

Értékkészlet: [; ]
A maximum helye:

 2 pont 

6.

Adja meg egy konvex 8-szög átlóinak számát!

Az átlók száma =

 2 pont 

7.

Adja meg x értékét három tizedesjegyre kerekítve, ha 10^x = 30.

x =

 2 pont 

8.

A valós számok halmazán értelmezett x ↦ 5x − 3 függvény grafikonja a P pontban metszi az x tengelyt.
Adja meg a P pont első koordinátáját!

x =

 2 pont 

9.

Rajzoljon egy olyan hatpontú gráfot, melyben két pontnak egyenlő a fokszáma, a többi négy fokszám viszont ettől és egymástól is különbözik!

Nem egyszerű gráf megoldás betűjele: A B C

 2 pont 

10.

Számítsa ki az alábbi háromszögben a 30°-os szöggel szemközti oldal hosszát!
Megoldását részletezze!

β = °
Szinusz-tétel:
a/ = sin°/sin °
a = cm

 2 pont 

11.

Egy minőségellenőr megszámolta hat gyufásdobozban a gyufaszálak számát.
A kapott adatokat az alábbi táblázat tartalmazza.
Számítsa ki az adatok átlagát és szórását!

doboz	első	második	harmadik	negyedik	ötödik	hatodik
szálak száma (db)	43	40	42	39	40	36

Az átlag:
A szórás: √()

 2 pont 

12.

Egy szabályos dobókockával kétszer dobunk.
Mennyi a valószínűsége annak, hogy a két dobott szám szorzata 6 lesz?
Megoldását részletezze!

k =
n =
A valószínűség:%

 2 pont 

Matematika középfokú érettségi (2022.október)

NÉV:

EREDMÉNYEK:

Feladat	Max pont	Elért pont	Paraméterek	Bemenet
1.	2
2.	2
3.	2
4.	3
5.	2
6.	2
7.	2
8.	2
9.	3
10.	3
11.	4
12.	3
Össz.	30		-	-

Főoldal (Érettségik)

Év	Május	Idegen nyelvű	Október	Egyéb
2022.	2022_05 ✓	2022_06 ⊕	2022_06 ⊕	2022_02 PDF
2021.	2021_05 ✓	2021_06 ⊕	2021_10 ⊕	2021_02 PDF
2020.	2020_05_1 ✓ 2020_05_2 ✗	2020_06 ⊕	2020_10 ⊕	2020_02 PDF 2020_02 próba ✗
2019.	2019_05_1 ✓ 2019_05_2 ✗	2019_06 ⊕	2019_10 ⊕	2019_02 PDF 2019_02 próba ✗
2018.	2018_05_1 ✓ 2018_05_2 ✗	2018_06 ⊕	2018_10 ⊕	2018_02 PDF
2017.	2017_05 ♥ 2017_05 ✓	2017_06 ⊕	2017_10 ⊕	2017_02 PDF
2016.	2016_05 ✓	2016_06 ⊕	2016_10 ⊕	Egyéb
2015.	2015_05 ✓	2015_06 ⊕	2015_10 ⊕	Egyéb
2014.	2014_05 ✓	2014_06 ⊕	2014_10 ⊕	Egyéb
2013.	2013_05 ✓	2013_06 ⊕	2013_10 ⊕	Egyéb
2012.	2012_05 ✓	2012_06 ⊕	2012_10 ⊕	Egyéb
2011.	2011_05 ✓	2011_06 ⊕	2011_10 ⊕	Egyéb
2010.	2010_05 ✓	2010_06 ⊕	2010_10 ⊕	Egyéb
2009.	2009_05 ✓	2009_06 ⊕	2009_10 ⊕	Egyéb
2008.	2008_05 ✓	2008_06 ⊕	2008_10 ⊕	Egyéb
2007.	2007_05 ✓	2007_06 ⊕	2007_10 ⊕	Egyéb
2006.	2006_05 ✓	2006_06 ⊕	2006_10 ⊕	2006_2 ⊕
2005.	2005_05 ✓	2005_06 ⊕	2005_10 ⊕	2005_07 ⊕
2003/2004. (minta)	-	-	-	2004 ⊕ 2003 ⊕
NKP. (próba)	-	-	-	1. feladatsor 2. feladatsor 1. feladatsor 2. feladatsor 1. feladatsor

Tömörített PDF letöltés: Feladatsorok

2006. február 1. rész

2006. február Matematika - középszint I.

1.

Mennyi annak a mértani sorozatnak a hányadosa, amelynek harmadik tagja 5, hatodik tagja pedig 40?

, , .
A mértani sorozat hányadosa:
q =

 2 pont 

2.

Döntse el mindegyik egyenlőségről, hogy igaz, vagy hamis minden valós szám esetén!
A) b³ + b⁷ = b¹⁰
B) (b³)⁷ = b²¹
C) b⁴b⁵ = b²⁰

A) logikai értéke minden valós számra:
B) logikai értéke minden valós számra:
C) logikai értéke minden valós számra:

 2 pont 

3.

Mekkora x értéke, ha lg x = lg 3 + lg 25 ?

x =

 2 pont 

4.

Hány különböző háromjegyű pozitív szám képezhető a 0, 6, 7 számjegyek felhasználásával?

féle szám képezhető.

 2 pont 

5.

Egy öttagú társaság egymás után lép be egy ajtón.
Mekkora a valószínűsége, hogy Anna, a társaság egyik tagja, elsőnek lép be az ajtón?

A valószínűség: %

 2 pont 

6.

Tekintse a következő állításokat, és a táblázatban mindegyik betűjele mellé írja oda, hogy igaz, vagy hamis állításról van-e szó!
A: Két pozitív egész közül az a nagyobb, amelyiknek az abszolút-értéke nagyobb.
B: Két egész szám közül az a nagyobb, amelyiknek az abszolút-értéke nagyobb.
C: Negatív szám egész kitevőjű hatványai között pozitívak és negatívak is vannak.

A. állítás logikai értéke:
B. állítás logikai értéke:
C. állítás logikai értéke:

 2 pont 

7.

Melyek azok az x valós számok, amelyekre nem értelmezhető az 1/(x² -9) tört? Válaszát indokolja!

x² ≠
x1 ≠
x2 ≠

 2 pont 

8.

Rajzoljon egy olyan öt csúcspontú gráfot, amelyben a pontok fokszáma 4; 3; 3; 2; 2.

Melyik él hiányzik az ábráról?
él.

 2 pont 

9.

Jelölje meg annak a kifejezésnek a betűjelét, amelyik az ax² + dx + e = 0 egyenlet diszkriminánsa, ha a ≠ 0 .
a) d² − ae
b) d² − 4ae
c) √(d² - 4ae)

A keresett betűjel:

 2 pont 

10.

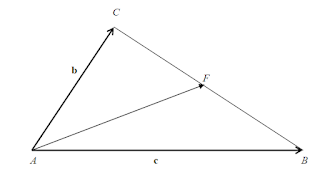
Az ABC háromszög két oldalának vektora (AB) = c és (AC) = b.

Fejezze ki ezek segítségével az A csúcsból a szemközti oldal F felezőpontjába mutató (AF) vektort!

(AF) =

 2 pont 

11.

Egy farmernadrág árát 20%-kal felemelték, majd amikor nem volt elég nagy a forgalom, az utóbbi árat 25%-kal csökkentették.
Most 3600 Ft-ért lehet a farmert megvenni.
Mennyi volt az eredeti ára?
Válaszát számítással indokolja!

Ha x Ft a farmer eredeti ára, akkor
x·· =
x = Ft

 2 pont 

12.

Az A és a B halmazokról a következőket tudjuk:
A ∩ B = {1; 2},
A∪B = {1; 2; 3; 4; 5; 6; 7},
A \ B = {5; 7}.
Adja meg az A és a B halmaz elemeit!

A = {}
B = {}

 2 pont 

Matematika középfokú érettségi (2006.február)

NÉV:

EREDMÉNYEK:

Feladat	Max pont	Elért pont	Paraméterek	Bemenet
1.	2
2.	2
3.	2
4.	3
5.	2
6.	2
7.	2
8.	2
9.	3
10.	3
11.	4
12.	3
Össz.	30		-	-

2005. július 1. rész

2005. július Matematika - középszint I.

1.

Mely x valós számokra igaz, hogy x² = 9 ?

x1 =
x2 =

 2 pont 

2.

Egy háromszög egyik oldalának hossza 10 cm, a hozzá tartozó magasság hossza 6 cm.
Számítsa ki a háromszög területét!

A háromszög területe cm²

 2 pont 

3.

Egy vállalat 250 000 Ft-ért vásárol egy számítógépet.
A gép egy év alatt 10%-ot veszít az értékéből.
Mennyi lesz a gép értéke 1 év elteltével?
Írja le a számítás menetét!

Záróérték = (1 - /100)^
A gép értéke: Ft lesz.

 2 pont 

4.

Számítsa ki az α szög nagyságát az alábbi derékszögű háromszögben!

sin α = /
α = °

 2 pont 

5.

a) Rajzolja fel a [− 3;3] intervallumon értelmezett x ↦ |x| −1 függvény grafikonját!
b) Mennyi a legkisebb függvényérték?

a) Táblázat:

x	-3	0	3
y

b) Minimum értéke: y =

 2 pont 

6.

Melyik az az x természetes szám, amelyre log ₃ 81 = x ?

x =

 2 pont 

7.

Egy dobozban 50 darab golyó van, közülük 10 darab piros színű.
Mennyi annak a valószínűsége, hogy egy golyót véletlenszerűen kihúzva pirosat húzunk?
(Az egyes golyók húzásának ugyanakkora a valószínűsége.)

p = %

 2 pont 

8.

Adja meg azoknak a 0° és 360° közötti α szögeknek a nagyságát, amelyekre igaz az alábbi egyenlőség!
 cosα = 1/2 .

α1 = °
α2 = °

 2 pont 

9.

Melyik az ábrán látható egyenes egyenlete az alábbiak közül?
A: y = 2x + 3.
B: y = −2x + 3.
C: y = 2x −1,5.
D: y = 2x − 3.

A helyes válasz betűjele:

 2 pont 

10.

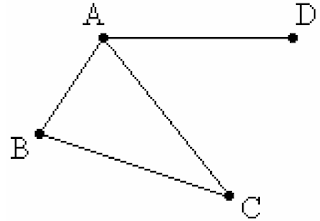
Egy álláshirdetésre négyen jelentkeznek: Aladár, Béla, Cecil és Dénes.
Az adott időben megjelennek a vállalatnál, s akkor kiderül, hogy közülük hárman, Aladár, Béla és Cecil osztálytársak voltak.
Dénes csak Aladárt ismeri, ők régebben egy kosárlabdacsapatban játszottak.
Szemléltesse az ismeretségeket gráffal! (Az ismeretségek kölcsönösek.)

Ez az ábra megfelelő-e?

 2 pont 

11.

Egy henger alakú bögre belsejének magassága 12 cm, belső alapkörének átmérője 8 cm.
Belefér-e egyszerre ½ liter kakaó?
Válaszát indokolja!

V = ²·π·
V = cm³
Válasz: Belefér-e?

 2 pont 

12.

Három tömör játékkockát az ábrának megfelelően rakunk össze.
Mindegyik kocka éle 3 cm.

Mekkora a keletkező test
a) felszíne,
b) térfogata?
Számítását írja le!

a)
Egy lap területe cm².
A felszín lap területének összege.
A felszín cm²
b)
A keletkező test térfogata cm³

 2 pont 

Matematika középfokú érettségi (2005.július)

NÉV:

EREDMÉNYEK:

Feladat	Max pont	Elért pont	Paraméterek	Bemenet
1.	2
2.	2
3.	2
4.	3
5.	2
6.	2
7.	2
8.	2
9.	3
10.	3
11.	4
12.	3
Össz.	30		-	-